Neural Approach to the Discovery Problem in Process Mining

备注

• 算法没完全理解
• 日志到向量？

一、文章速览

1.论文信息

时间-题目-作者-出版社-影响因子

(2018). Neural Approach to the Discovery Problem in Process Mining.Shunin, T., Zubkova, N., & Shershakov, S. AIST. https://doi.org/10.1007/978-3-030-11027-7_25

2.背景

过程挖掘处理各种形式模型。其中一些用于合成和分析的中间阶段，而另一些则是预期目标本身。变迁系统(TS)在这两种场景中被广泛使用。

3.方法

本文提出了一种基于循环神经网络RNN的新方法。使用事件日志作为训练集，提取RNN的中间状态作为TS来描述日志中的行为。
特点：

• 模型适合度高。包含了日志中的所有行为、简洁、精确。
• 神经方法的主要优点之一是能够检测和合并分散在日志中的常见行为部分。

4.概述

我们研究的主要目标之一是分析所提方法的效率，即，看看不同的质量度量如何依赖于输入数据和用户指定的参数。
主要贡献如下:

• (1) 描述和实现了一种使用循环神经网络建立变迁系统的方法;

• (2) 将所述方法构建的模型质量度量与基于频率约简算法(FQR)[10]和前缀树[3]推导的模型质量度量进行比较;

• (3) 总结事件日志的特性，其中RNN方法比FQR方法有更好的结果。

  算法步骤见第二部分。

适合度高。这种方法通过构造合成完全适合的FSM(即它们总是可以重放整个日志)。用与[10]中定理1相同的步骤，用归纳法很容易地证明它。
能够控制创建的状态和变迁。这使得我们可以制作出不完全匹配的模型，尽管给了它们其他的特性，例如对噪声的鲁棒性。这为进一步的研究提供了坚实的基础，因为有很多方法可以分析上面提到的标识概率的预测。

超参数。上述神经网络有一个超参数：密集层中的神经元数量。每增加一个神经元，不仅直接影响学习质量，而且使输出状态空间增加一倍。从技术上讲，模型有更多的超参数。输出矢量中的神经元数目和前面提到的嵌入方法也可以看作是这样的。我们认为它们不那么重要，因此在我们的实验中将它们排除在外。然而，在进一步的实验中可以考虑它们。

5.局限

未充分利用神经网络处理噪音数据的能力。在本文中，我们仅为日志构建了完全适合的TSs，因此可能还没有发现此方法的全部潜力。

6.未来方向

需要对不需要完美拟合模型的任务领域进行进一步研究，以便找到可以使用这种模型的任务。如果我们考虑这个方法，可以考虑网络内层的不同架构，因为现在只对一个简单的神经网络进行实验，只有一个隐藏的稠密层。此外，使用5.2中提到的技术处理过拟合可能提供更好的结果。

---

二、方法的具体描述

1. 预备知识

(1)过程挖掘相关概念

• A：流程产生的活动集

• An event e：日志中某个活动的发生

• A token：传递给神经网络的日志的一个元素。

  **文中假设一个事件event和一个标识token是在不同上下文中使用的同义词。**与平时见到的不一样。

• Λ：日志的所有唯一事件的集合Λ被称为输入字母(A set Λ of all unique events of the log is called an input alphabet.)。

• |Λ|：表示输入字母的基数。

• A+：是A上所有非空有限序列的集合。

(2)神经网络

• 结构。

  包含三个主要部分：输入层、隐层和输出层。每一层都是一组神经元，每个神经元都是一个计算单元，对流经它的数据应用某些激活函数。这些层是通过有权重的连接联系起来的，这些连接将信号从一层的神经元传输到下一层的一个或多个神经元。传递到输入层的数据的最终变迁应该满足网络所解决的问题所隐含的条件。在神经网络中，这种情况用一个损失函数来表示。为了实现这种变迁，绑定连接的权重被配置。

• 学习。配置权重的过程称为学习或训练过程。它包括优化损失函数，或误差，使用反向传播[12]。在每次训练迭代中，当前的误差被传播到前一层，在那里它被用来修改权值，以使误差最小化。在[1]Bishop对神经网络中存在的计算的意义和目的提供了更完整的见解。

• 超参数。在学习过程中，神经网络的一些参数不能得到优化，也会影响计算结果。这样的参数称为超参数，应该在学习过程开始之前定义。隐层中的神经元数就是这样一个参数。

本文所描述的方法是基于循环神经网络的(RNN)。这样的网络有一个或多个循环连接连接输出层和输入层，这允许网络使用它之前的计算来进行下面的预测。RNN的训练通常与普通神经网络的训练相似，通常涉及随机梯度下降[12]。

2.神经网络方法的描述

1. **预处理。**需要对数据进行预处理：将迹的长度补齐，开头和结尾分别添加’$'和‘#’。

   L =[<a, b, c, d, e>,<a, b, d>]–>L˜ =[<, a, b, c, d, e,#> , <,a,b,d,#,#,#>]。

   |L˜ |=7，将其用0~|Λ|+1=6进行编码。

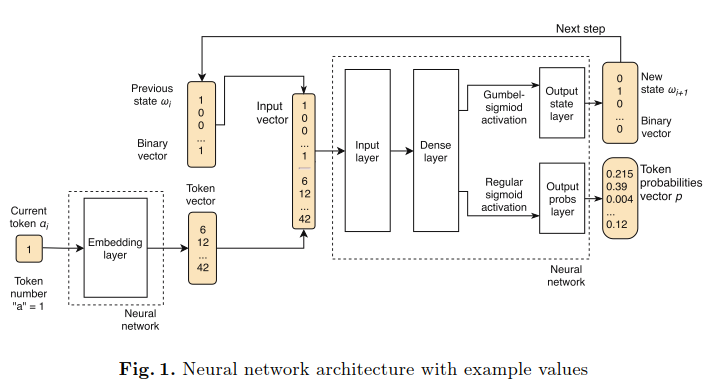
   如果将预测标识问题视为分类任务，就可以使用特定的方法和架构。对于每个标识(事件)，我们想要确定后面的标识的一类标识，即由它表示的一个活动。此外，我们应该考虑历史的迹;否则，预测将只依赖于之前的标记，这将导致学习单个事件之间的关系图。这就是出现周期性连接的原因，它构成了更复杂的输入向量。如果网络有能力生成可信的迹，那么内部状态，从中做出预测，是可信的，并且代表了迹的历史和当前标识，因此可以作为TS的一种状态。为了解决这个问题，我们开发了如图1所示的神经网络架构。

   

2. 算法架构解释

   • 嵌入层(embedding layer)：将迹中的下一个编码(整数)转换为一个标识向量。

   • 输入层(input layer)：包括以下两部分，随后应用一个线性变换，编程一个向量，进入密集(隐藏)层—dense(hidden) layer

     • 一个二元向量：表示前面状态
     • 标识向量

     对计算得到的向量应用不同的激活函数，从输出层提取两个不同的实体。

   • 输出层(output layer)

     • 一个新的离散二进制向量：由Gumbel Sigmoid函数计算得到，解释为RNN的新状态，并返回作为下一次迭代的新参数。

     • 标识概率p：应用regular sigmoid函数得到。将用于计算损失函数。

       

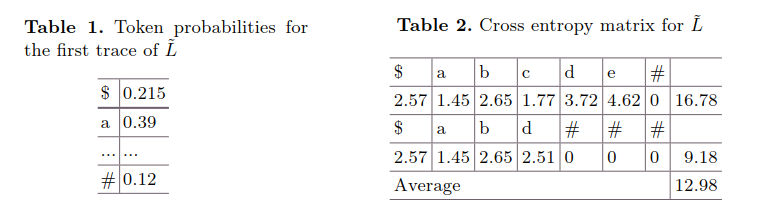
3. **损失矩阵。**构建mxr损失(交叉熵)矩阵-loss(cross entropy) matrix。

   • m：输入日志中的迹的数量

   • r：预处理的迹的最大长度。

     每一行对应一条迹，每个元素对应一条迹中的一个标识。每一步要计算元素的交叉熵H(yi^,yi)。

4. 舍弃无用符号。预处理时填充了一些符号，此时通过掩模矩阵(mask matrix)处理：实数对应‘1’；’$’、‘0’和’#‘对应’0’。然后将损失函数计算为每一行的和的平均值。

5. 训练的形式。将事件日志逐条地呈现给神经网络，通过随机梯度下降最小化上述损失函数，从而更新层间连接的权值。

6. 从神经网络方法推断FSM(有限自动机)的步骤。

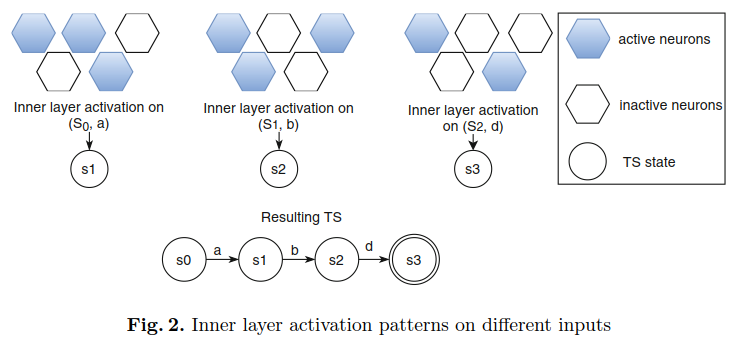
   • 神经网络的状态如何对应于合成的变迁系统的状态(图2)。

     

   • 定义三个双射函数，Ω → N, ψ : N → S and φ : Ω → S。

     • Ω：由输出层中神经元的状态表示的神经网络的一组状态。
     • ωi ∈Ω：我们表示循环神经网络在算法第i步的状态。
     • 双射函数ξ : Ω → N, ψ : N → S and φ : Ω → S 。ωi是二进制向量，ξ将其解释为一个二进制数，并将其转换为等效的十进制数；ψ 转换数字j从N到状态sj；φ是ψ和ξ的组合；Ω是通过N到S的同构。

   • TS = (S, E, T, s0, AS)的构造按照以下步骤进行。

     • 我们从把状态s0加到原来空的TS开始。神经网络的初始状态ω0是一个零向量。
     • 第i步时，RNN的当前状态是ωi ，新的输入标识是从原输入标识得到的αi。两者构成了RNN的输入向量，而输出向量分别为ωi+1和pi+1。
     • TS的当前状态是si=φ(ωi)；如果它不存在或以其他方式重用，那么下一个标识si+1 = φ(ωi+1)就添加到TS中。
     • 这些状态通过变迁ti=(si, αi, si+1)连接。
     • 对每个迹的所有非“#”标记重复以上步骤。

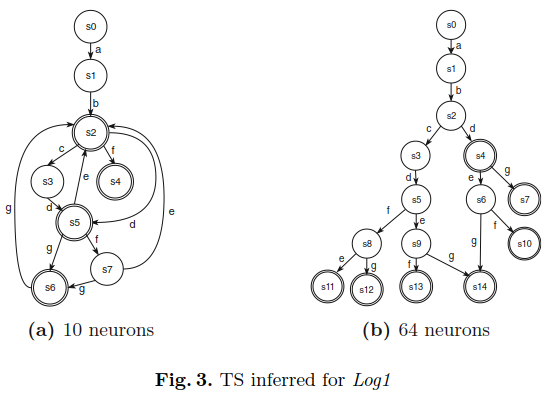
7. 删t0。提取的TS具有惟一的变迁t0 = (s0， $， s1)，这是因为我们用“$”标记了所有迹的开始。

   变迁和标识都具有纯技术性质，并且不包含与输入日志行为相关的任何有意义的信息。因此，我们可以简单地删除变迁t0，并将状态s1视为Ts的初始起始点。如果其他有效的变迁将状态s0连接到其他状态，则TS中仍然存在状态s0。图3给出了两个不同超参数值的Log1的TS提取示例。

   

---

三、他评

待续

---

下载：