Mining Process Models with Non-Free-Choice Constructs
一、文章速览
1.论文信息
题目-作者-时间-出版社-引用
Wen, Lijie et al. “Mining process models with non-free-choice constructs.” Data Mining and Knowledge Discovery 15 (2007): 145-180.
2.背景
现实生活中的许多进程不具有自由选择属性。因此,提供能够成功发现非自由选择结构的技术非常重要。目前存在的算法不能充分处理这样的结构。
3.方法
本文介绍了一种成功挖掘隐式依赖关系的方法α++ 。
4.概述
假设:
- (i) 日志必须是完整的
- (ii)日志是无噪声的
- (iii)日志中变迁名称唯一(无重名变迁)
本文关注挖掘非自由选择结构,即同时存在选择和同步的情况。使用基于Petri网的算法α++,可以挖掘非自有选择结构。即,一些非自由选择的Petri网可以被正确地发现。
5.局限
并非所有合理的工作流网都能成功地从其相应的事件日志中导出。
-
在N4 ={ABCE, ACBE, ABDDCE}中,A和D以及D和E之间都有隐式的依赖关系。任务D涉及到一阶循环和两个隐式依赖项。在定义6中,假设一阶循环中的任务不涉及任何隐式依赖。因此在定义的第4步和第5步中无法正确检测到连接到D的库所。
N5中的A与D,H与E存在隐式依赖,和N4类似。
以上可以通过定义3和5进行细微调整得到正确结果。但是也一些不能修复的。
-
(1) N6={ABDEHF I, ADBEHF I, ACDFGEI, ADCF GEI},只有在B和C之间的选择是自由选择的。H和E, G和F, E和G, F和H之间的顺序关系对于今天的任何挖掘算法来说都太困难了。
(2) N7,它的一个完整事件日志是{ABCE, ACDF, ADBG}。所有生成的事件跟踪都是基于B、C和D之间的选择。B和B、C和C、D和D、A和E、A和F、A和G之间的顺序关系更难挖掘。
上面的例子涉及相当复杂的结构,难于分解,但同时却很少见。从实用的角度来看,更重要的问题是与 噪声和完整性 有关的问题。
6.未来方向
- 将α算法应用于更多实际过程中
- 探索一些处理不完整性的技术
- 希望解决过程挖掘领域中的其他未解决问题,例如,不可见的任务(例如,跳过未记录的任务),重名的任务(即,模型中的不同任务无法在日志中区分 ),噪音(例如,处理异常行为或错误日志)等。
二、算法具体描述
1.问题描述
要从事件日志中直接提取具有非自由选择构造的流程模型,必须有一种挖掘所有依赖的方法。
- free-choice:自由选择Petri网是Petri网的一个子类,消耗来自相同库所标识的变迁应该具有相同的输入集。
- 两种因果依赖关系,即显性和隐性的。
-
**依赖分为两种类型:**显式依赖(直接依赖)和隐式依赖(间接依赖),定义如下。
定义1中,
s-·a+a·表示网N在发生a后的标识下可以到达b(其中-·a+a·表示a消耗的和a生成的标识的差值)。 -
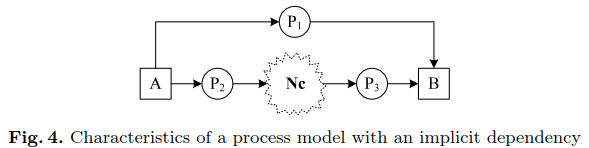
具有隐式依赖的过程模型具有什么特征?
假设A和之间存在隐式依赖关系,一旦执行了A,在执行B之前一定还有其他任务。之后,执行B。B永远不可能在某种程度上直接跟随A,因为“依赖距离”至少是2。所以A和B之间的隐式依赖使用经典的α方法不能直接检测到,比如使用弱序关系>。
隐式库所不会影响流程模型的行为,即,可以在不改变可达状态集的情况下删除它们。如果没有其他任务连接到P1、P2和P3, P1将成为一个隐式库所。虽然添加它们是无害的,但我们更喜欢避免构造隐式库所的挖掘算法。请注意,并非所有隐式依赖都对应于隐式库所。下面将图4所示的基本情况的扩展为图5。
在本文中,我们将考虑三种情况:
-
图5中的模式(b)和(g)所描述的情况,其中,α算法错误地将库所P1替换为两个或多个库所。
-
模式©, (d), (e)和(f)所描述的情况,在这种情况下,α算法漏掉了A和P1 (A, P1)或P1和B (P1, B)之间的弧线。
-
模式(a)所描述的P1库所根本没有被发现的情况。
-
2.检测隐式依赖
-
显式依赖用α算法挖掘
-
隐式依赖
改进阿尔法中的定义——高级序关系
-
序关系(>w反映了长度为1的关系,>>w反映长度为2及以上的关系)
示例:对于{T1T3T4, T2T3T5},任务之间的高级排序关系为
-
完全事件日志
-
隐式序关系
不同类型日志中的隐式依赖关系:
- 类似图5(b)和(g)。 →W1:确保一旦在挖掘的模型中存在连接两个连续变迁的库所,而后一个任务具有多个输入库所**,则后一个任务始终可以有机会在前一个任务之后直接执行。
- 类似图5©-(f)。 →W2:如果任务从多个并行分支之一获取标识,则它及其并行任务也必须消耗其他分支的标识**。
- 类似图5(a)。 **→W3:如果两个排他任务(即XOR联接中涉及的任务)导致了不同的并行分支集,并且这两个集合及其任务满足一定条件,则挖掘的工作流网仍然是正确的。
-
3.挖掘算法
-
首先分析上一节中提出的三种隐式序关系之间的相互关系。检测的顺序如下:
-
然后,我们引入两个归约规则,以消除那些导致冗余隐式依赖的隐式排序关系。
不是所有的隐式依赖都是有意义的,因此引入约简规则进行简化,目的是消除所有非基本的隐式依赖,同时保留基本的依赖。
-
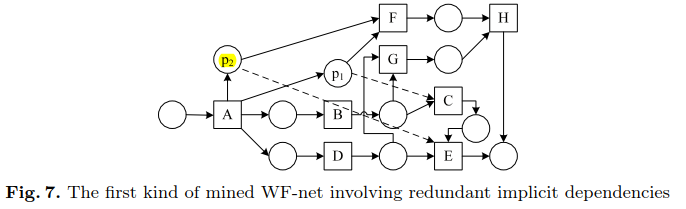
第一种涉及冗余隐式依赖的类型及约简规则1——通过消除相关的隐式排序关系
-
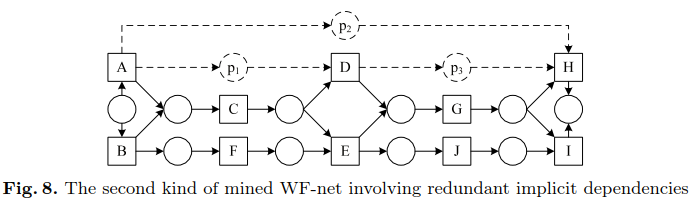
第二种涉及冗余隐式依赖的类型及约简规则2——根据所有基本隐式依赖的传递闭包来消除距离较长的隐式依赖
-
-
随后,给出了一种名为α++的挖掘算法,用于使用涉及隐式依赖性的非自由选择构造来构造过程模型。
算法的解释:
- 步骤1到3直接借鉴了[42]
- 步骤4、5中,确定了连接一阶循环变迁的库所,并将其包含在LW中。
- 步骤6、7,从输入日志W中删除所有一阶循环变迁,并推导出新的输入日志W‘(方便起见,把W-L1L记作W’),用α算法处理
- 步骤8,检测W’中的所有隐式排序关系→W1
- 步骤9中,α算法基于W’和定义3中定义的排序关系发现WF网
- 步骤10到13,所有涉及→W1和→W2关系的库所都被导出并包含在YW中。 首先,一旦将IDW1中的所有→W1都视为→W,就检测到W中的所有隐式依赖性→W2(步骤10)。 然后应用规则1来减少IDW2中的冗余隐式依赖性(步骤11)。 最后,所有涉及前两种隐式依赖关系的库所都从PW’(将PW−L1L记作PW‘)导出,而保留PW’中的其他库所(步骤12和13)。
- 步骤14到17,所有与→W3关系有关的库所都被导出并包含在ZW中。 首先,将IDW2中的所有→W2视为→W,并检测W’中的所有隐式依赖性→W3(步骤14)。 然后应用规则2来减少IDW3中的冗余隐式依赖关系(步骤15)。 最后,所有基于第三种隐式依赖关系的场所都是基于这些→W3关系得出的(步骤16和17)。
- 步骤18到20,收集了已挖掘的WF网络中的所有库所,并将一阶循环的变迁添加到了网中,并且还导出了网的所有弧。
- 步骤21,返回带有非自由选择结构、一阶循环和隐式依赖项的工作流网
-
最后,我们简要讨论了α++算法的复杂性。
α算法是由> W,△W和≫W关系驱动的,其构建时间是线性的。而α算法中其余步骤的复杂度在任务数量上呈指数级增长。但是通常任务数量较少,因此瓶颈不在于复杂度。真正的限制因素是模型的可视化和分析人员对模型的解释。
三、他评
下载: